由于个人能力问题，仅写出A-E的题解。

A Cards for Friends

题意

给出大小w*h 的纸，要用这张纸分割为n张贺卡，如果任意一边边长为偶数，则可以一分为二，，为奇数则不可以。然后得到的两张纸可以按照该规则继续分割。

题解

我们只需要求出能分割最大数目就可以了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
int main(void)
{
    int _;
    cin>>_;
    while(_--){
        int w,h,n,num=1;
        cin>>w>>h>>n;
        while(w%2==0&&w!=1){
            w=w/2;
            num=num*2;
        }
        while(h%2==0&&h!=1){
            h=h/2;
            num=num*2;
        }
        if(num>=n) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;

    }
}

B Fair Division

题意

Alice和Bob分一堆糖果，糖果只有1g和2g的规格（糖果不可分割），问能否平均分给二人。

题解

特判即可，只需考虑2种情况：
1.2g为偶数的时候1g也为偶数。（1g为奇数就不可能平均分）
2.2g为偶数的时候1g也为不为0的偶数。（因为2g平均分之后最多差2，所以可以用2个1g的补回来，但是为0的时候就不能补了。）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
int main(void)
{
    int _;
    cin>>_;
    while(_--){
        int n;
        cin>>n;
        int n1=0,n2=0,s;
        for(int i=0;i<n;i++){
            cin>>s;
            if(s==1) n1++;
            if(s==2) n2++;
        }
        if(n2%2==0){
            if(n1%2==0){
                cout<<"YES"<<endl;
                continue;
            }
        }
        else{
            if(n1%2==0&&n1!=0){
                cout<<"YES"<<endl;
                continue;
            }
        }
        cout<<"NO"<<endl;
    }
}

C Long Jumps

题意

一个跳远游戏，我们可以选择数组中任意一点起跳，跳的距离和增加的分数均为该点的值，若跳出数组，游戏结束，求能得到的最大分数。

题解

开一个用于暂时储存分数的数组，遍历一遍。如果没有跳出去，就存在数组里面（当有多个路线跳到同一点的时候，仅保留最大值）。如果跳出去，就得到最终分数，同样保留最大值。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
ll max(ll a, ll b) {
    if (a > b) return a;
    return b;
}
int main(void)
{
    int _;
    cin>>_;
    while(_--){
        ll n,s,re=0;
        cin>>n;
        ll num[n+1];
        memset(num,0,sizeof(num));
        for(int i=1;i<=n;i++){
            cin>>s;
            if(s-(n-i)>0){
                re=max(s+num[i],re);
            }
            else{
                num[i+s]=max(num[i+s],num[i]+s);
            }
        }
        cout<<re<<endl;
    }
}

D Even-Odd Game

题意

在一个数组中，Alice取偶数得分，取奇数不得分，而Bob正好相反。Alice总是先手，二人都是最佳发挥，求最终谁获胜。

题解

一个贪心，Alice可以取一个偶数让自己得分，也可以消除一个奇数阻止Bob得分，Bob同理。将奇数和偶数分别存在两个vector容器里面，当消除的数大于得分的数、或无法得分（即数组为空）的时候，则消除，否则得分。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
int main(void)
{
    int _;
    cin>>_;
    while(_--){
        ll n,s;
        cin>>n;
        ll alice=0,bob=0;
        vector<ll> j;
        vector<ll> o;
        for(int i=0;i<n;i++){
            cin>>s;
            if(s%2==0) o.push_back(s);
            else j.push_back(s);
        }
        sort(j.begin(),j.end());
        sort(o.begin(),o.end());
        while(o.size()!=0||j.size()!=0){
           if(o.size()!=0){
                if(j.size()!=0&&j.back()>o.back()){
                    j.pop_back();
                }
                else{
                    alice+=o.back();
                    o.pop_back();
                }

           }
           else if(j.size()!=0){
            j.pop_back();
           }
           if(j.size()!=0){
                if(o.size()!=0&&o.back()>j.back()){
                    o.pop_back();
                }
                else{
                    bob+=j.back();
                    j.pop_back();
                }

           }
           else if(o.size()!=0){
                o.pop_back();
           }
        }
        if(alice>bob) cout<<"Alice"<<endl;
        else if(alice==bob) cout<<"Tie"<<endl;
        else cout<<"Bob"<<endl;
    }
}

E Correct Placement

题意

一群人在拍照，每一个人都有一个宽度w和高度h，一个人可以选择站着或躺着。(w₁<w₂&&h₁<h₂)||(w₁<h₂&&h₁<w₂)成立的时候，就认为1可以站在2的前面。对于每一个人，输出任意一个可以站在他前面的人的下标，如果没有则输出-1。

题解

我们可以把h,w中的最小值看作h，最大值看作w。然后按照先h后w排序，这时候后面的h保证小于等于前面的h，当h发生变动时，查找此前最小的w，并记录下标。
示例：

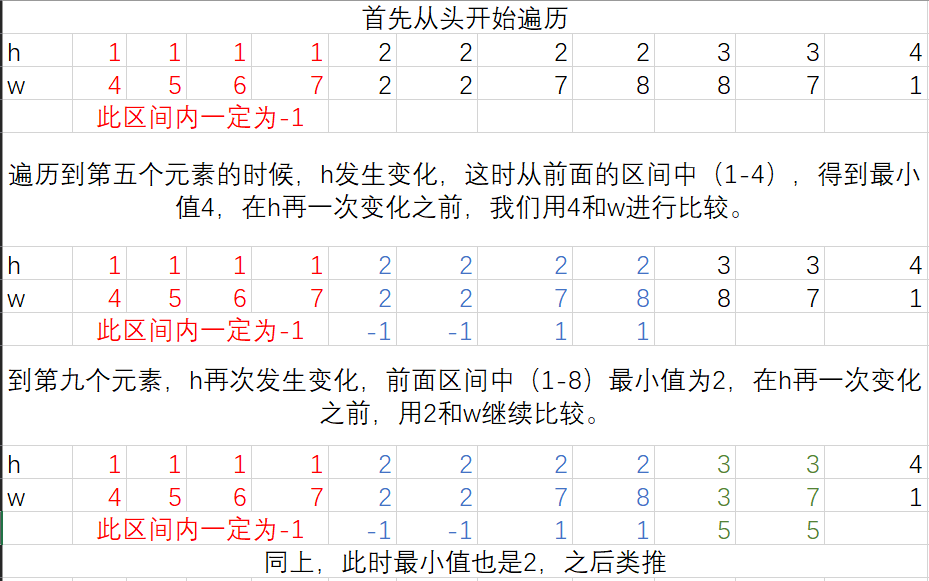
此代码还可以在查找最小值上继续优化。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
struct node{
    int h;
    int w;
    int i;
    bool operator < (node a){
        if(h!=a.h)
            return h < a.h;
        return w < a.w;
    }
};


int main(void)
{
    int _;
    cin>>_;
    while(_--){
        int n,h,w;
        cin>>n;
        vector<node> num;
        for(int i=1;i<=n;i++){
            node a;
            cin>>h>>w;
            a.h=min(h,w);
            a.w=max(h,w);
            a.i=i;
            num.push_back(a);
        }
        sort(num.begin(),num.end());
        int re[n+1];
        int minw=imax,mini=-1;
        int start=num.front().h;
        int startj=0;
        for(int i=0;i<n;i++){
            if(start!=num[i].h){
                start=num[i].h;
                int j=startj;
                startj=i;
                for(;j<startj;j++){
                    if(num[j].w<minw){
                        minw=num[j].w;
                        mini=num[j].i;
                    }
                }
            }
            //cout<<num[i].w<<" "<<num[i].i<<" "<<minw<<" "<<mini<<endl;
            if(num[i].w>minw) re[num[i].i]=mini;
            else re[num[i].i]=-1;
        }
        for(int i=1;i<=n;i++){
           cout<<re[i]<<" ";
        }
        cout<<endl;
    }
}

题目来源于https://codeforces.com/contest/1472