括号位置放错了,C一直WA3,气死了,这场每题都在犯der。
A. K-divisible Sum
题意
由n个正整数组成的数组的和要整除k,求数组中的最大值。
题解
n和k搞反了,同时n>k考虑不周WA了两发,签到题都开始WA了。
k=1的时候,任何数都能整除1,直接输出1。
当n>k的时候,数组内一定只有1和2(因为和为k的倍数)。
n<=k的时候,就是k/n向上取整(要使得数最小,就必须接近平均,但不能出现小数只好向上取整。)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int _;
cin>>_;
while(_--){
ll n,k;
cin>>n>>k;
if(k==1){
cout<<1<<endl;
continue;
}
if(n>k){
if(n%k) cout<<2<<endl;
else cout<<1<<endl;
}
else{
if(k%n) cout<<k/n+1<<endl;
else cout<<k/n<<endl;
}
}
return 0;
}
B. Inflation
题意
给出一个产品价格变化表,我们可以增加表中的任意数字,使得每个月的通货膨胀系数(\frac{p[i]}{\sum^{i-1}_ {i=0}p[i]}(i>0))小于等于k%,求最小增加的值。
题解
找出最大的通货膨胀系数,计算出让他小于等于k%需要增加的值即可,让最大的系数小于等于k,也就意味着所有的都会小于等于k%。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int _;
cin>>_;
while(_--){
int n,k;
cin>>n>>k;
vector<ll> num;
ll s,sum=0;
ll f=0;
for(int i=0;i<n;i++){
cin>>s;
num.push_back(s);
//cout<<s*100<<" "<<k*sum<<endl;
if(i!=0){
if(s*100>k*sum) f=max(f,s*100-k*sum);
}
sum+=s;
}
//cout<<f<<endl;
if(f==0) cout<<0<<endl;
else {
if(f%k)cout<<f/k+1<<endl;
else cout<<f/k<<endl;
}
}
return 0;
}
C. Longest Simple Cycle
题意
有n条链子,长度c[i],从第二条开始,每条的第一个节点连接前一条的a[i]节点,最后一个结点连接前一条的b[i]节点,求连接后最长的简单环。
题解
贪心。
首先求出第一条链子能记入环的节点数,因为a[i]和b[i]的大小关系不确定,所以要加绝对值。
然后从第二条链子开始遍历,每次成环都可以以当前链子为终点,所以加上当前链子的长度。
当我们继续遍历的时候,有两种情况:
1.a[i+1]=b[i+1],这种意味着下一条链子前后连接到同一个点上,只能作为环的起始或终止。
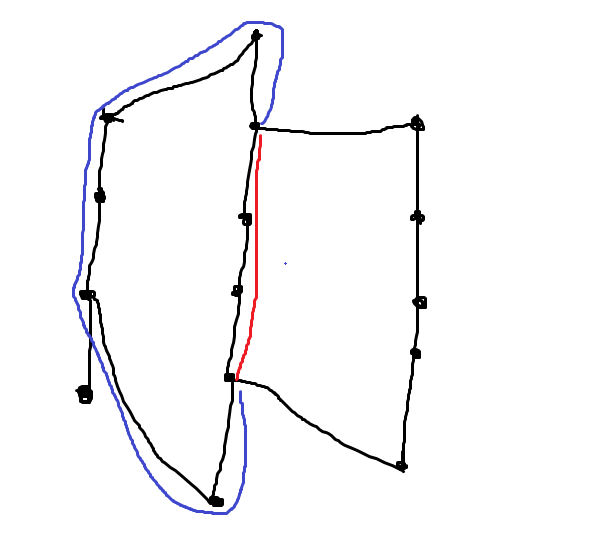
2.a[i+1]!=b[i+1],这时候我们可以选择下一条链子的两个连接点的中间(如下图红色部分),也可以选择两边+前面的链子(如下图蓝色部分),我们取最长的。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int _;
cin>>_;
while(_--){
int n;
cin>>n;
ll lon[n];
ll con1[n];
ll con2[n];
ll re=0;
ll s;
for(int i=0;i<n;i++) cin>>lon[i];
for(int i=0;i<n;i++) cin>>con1[i];
for(int i=0;i<n;i++) cin>>con2[i];
s=abs(con1[1]-con2[1])+1;
for(int i=1;i<n;i++){
//cout<<s<<" "<<s+lon[i]<<endl;
re=max(re,s+lon[i]);
if(i==n-1) break;
if(con1[i+1]==con2[i+1]){
s=1;
}
else s=max(s+lon[i]-abs(con1[i+1]-con2[i+1])+1,abs(con1[i+1]-con2[i+1])+1);
}
cout<<re<<endl;
}
return 0;
}
D. Journey
题意
有n+1个城市在一条直线上,中间有n条道路,每条道路都有方向,只能走导入方向和行进方向相同的道路,问最多经过几个城市。
题解
求每个点向左和向右的最大距离,相加即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f
void swap(ll* a, ll* b) {
int swapp = *a;
*a = *b;
*b = swapp;
}
ll max(ll a, ll b) {
if (a > b) return a;
return b;
}
ll min(ll a, ll b) {
if (a < b) return a;
return b;
}
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int lcm(const int a, const int b)
{
return a / gcd(a, b) * b;
}
bool isprime(ll num)
{
if (num == 1)
return 0;
if (num == 2 || num == 3)
return 1;
if (num % 6 != 1 && num % 6 != 5)
return 0;
int tmp = sqrt(num);
for (ll i = 5; i <= tmp; i += 6)
if (num % i == 0 || num % (i + 2) == 0)
return 0;
return 1;
}
struct node{
int top;
int bottom;
int num;
/*bool operator < (node a){
if(h!=a.h)
return h < a.h;
return w < a.w;
}
*/
};
bool check(ll num,ll d){
while(num!=0){
if(num%10==d) return 1;
else num=num/10;
}
return 0;
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int _;
cin>>_;
while(_--){
int n;
cin>>n;
string s;
cin>>s;
int numf[n+1];
int numb[n+1];
memset(numf,0,sizeof(numf));
memset(numb,0,sizeof(numb));
int f=0,i;
for(i=0;i<=n;i++){
if(i!=0&&((s[i-1]=='L'&&s[i]=='L')||(s[i-1]=='R'&&s[i]=='R'))){
int fl=0;
for(int j=i-f;j<i;j++){
if(fl%2==0)numf[j]=f;
fl++;
f--;
}
f=0;
}
if(s[i]=='R') f++;
else if(i!=0&&s[i-1]=='R'&&s[i]=='L')f++;
}
int fl=0;
for(int j=i-f;j<i;j++){
if(fl%2==0)numf[j-1]=f;
fl++;
f--;
}
f=0;
for(i=n;i>=0;i--){
if(i!=n&&((s[i+1]=='L'&&s[i]=='L')||(s[i+1]=='R'&&s[i]=='R'))){
int fl=0;
for(int j=i+f;j>i;j--){
if(fl%2==0)numb[j+1]=f;
fl++;
f--;
}
f=0;
}
if(s[i]=='L') f++;
else if(i!=n&&s[i+1]=='L'&&s[i]=='R')f++;
//cout<<f<<endl;
}
fl=0;
for(int j=i+f;j>i;j--){
if(fl%2==0)numb[j+1]=f;
fl++;
f--;
}
for(int i=0;i<n+1;i++) cout<<numf[i]+numb[i]+1<<" ";
cout<<endl;
}
return 0;
}

